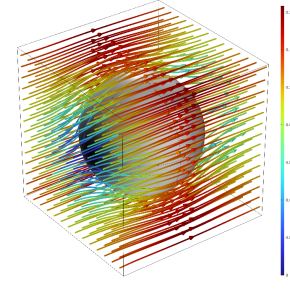
Milieux poreux : les limites minimales et maximales de la perméabilité
Il peut être utile de connaître les bornes inférieures et supérieures de la perméabilité d’un matériau poreux. Des chercheurs ont montré que celles-ci sont intrinsèques au matériau et définies respectivement par le cisaillement et le glissement maximaux du fluide traversant. Publiés dans le Journal of Fluid Mechanics, ces travaux pourraient trouver des applications dans l’élaboration de matériaux composites et de structures poreuses ainsi que dans l’estimation de la tenue de structures géologiques au stockage de gaz.
Lorsqu’un fluide s’écoule à travers un milieu poreux, ce dernier présente une perméabilité qui est inversement proportionnelle à la résistance du matériau à laisser s’écouler le fluide. En d’autres termes, ce coefficient dépend du cisaillement du fluide, dû à son caractère visqueux, lorsqu’il s’écoule dans les pores du matériau. Classiquement, la perméabilité est évaluée en supposant que le fluide adhère aux parois des pores et, dans ce cas, elle ne dépend que de la structure interne du matériau, c’est-à-dire de la géométrie des pores. On qualifie alors la perméabilité d’intrinsèque ou d’absolue. Mais dans de nombreuses circonstances, le fluide peut subir un glissement aux parois des pores, comme pour un gaz ou un fluide qui mouille imparfaitement le squelette solide du milieu poreux. À l’inverse du cisaillement, cet effet de glissement contribue à augmenter la perméabilité. Des chercheurs de l’Institut de mécanique et d’ingénierie (I2M, CNRS/Arts et Métiers/Bordeaux INP/Univ. Bordeaux) et de l’Université autonome métropolitaine Iztapalapa (UAM Iztapalapa, Mexique) ont étudié en détail ce mécanisme et montré que la perméabilité du milieu est forcément comprise entre le cas où le glissement du fluide est nul et celui où il est total. La perméabilité intrinsèque représente alors une borne inférieure, qui correspond à la résistance maximale. La borne supérieure, qui est elle aussi une propriété intrinsèque du matériau, est celle de l’écoulement qui se produit avec un glissement parfait et donc sans cisaillement à la paroi.
L’équipe est partie des équations classiques de la mécanique des fluides pour établir un modèle physique macroscopique. Ce résultat fondamental de la mécanique des fluides en milieu poreux fournit les bornes entre lesquelles la résistance du matériau à l’écoulement visqueux est nécessairement comprise. Il trouve des applications dans des domaines comme l’élaboration de matériaux composites ou le design de structures poreuses, mais également dans la prédiction des scénarios de tenue de structures géologiques au stockage de CO2 ou d’hydrogène par exemple.
Les chercheurs comptent à présent étudier comment prédire le comportement d’une structure dont les parois des pores sont faites de surfaces ayant des propriétés de glissement hétérogènes. Ils souhaitent également analyser la possibilité de déterminer des conditions équivalentes de glissement de gaz multiespèces pour une texture donnée.
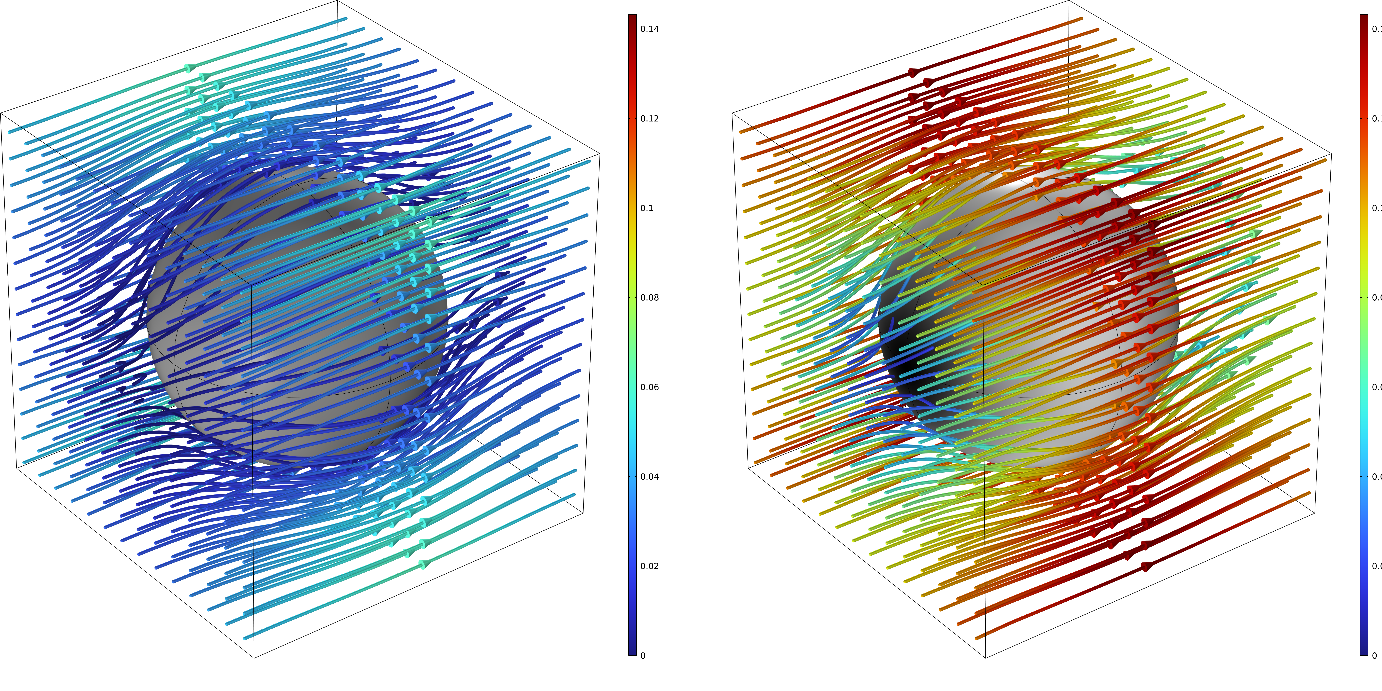
© Didier Lasseux
Références
Darcy’s law survival from no-slip to perfect-slip flow in porous media.
Didier Lasseux, Francisco J Valdés-Parada.
Journal of Fluid Mechanics, 997, A65, 2024.
https://doi.org/10.1017/jfm.2024.587
Article consultable sur la base d’archives ouvertes HAL
Voir aussi
Determination of Klinkenberg and higher-order correction tensors for slip flow in porous media.
Didier Lasseux, Tony Zaouter, Francisco J. Valdés-Parada.
Physical Review Fluids, 8, 053401, 2023.
https://doi.org/10.1103/PhysRevFluids.8.053401
Article consultable sur la base d’archives ouvertes HAL